Forces on a sliding block

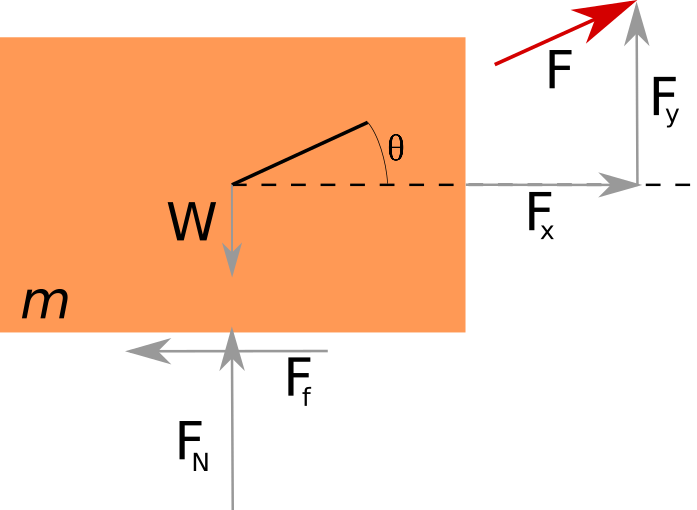
Given a weight \(W = 25 kN\), friction coefficient \(\mu = 0.75\), and angle of inclination \(\theta = 45^o\), calculate the force required to pull the block.

\[ F = \frac{\mu W}{\cos \theta + \mu \sin \theta} = \frac{\mu mg}{\cos \theta + \mu \sin \theta} \]

Python has a lot of useful standard library functions which are defined in modules. A Python code can gain access to the code in another module by the process of importing it. The import statement is the most common way of invoking the import machinery, but it is not the only way. We need to import a module called math, which has predefined trignometric functions using import math, this makes available all the functions in math module. To use the cos function in math module, we do math.cos(angle)

import math
mu = 0.75
angle = 45
theta = math.radians(angle)
W = 25
F = mu * W / (math.cos(theta) + mu * math.sin(theta))
print(F)

15.152288168283162

Bisection approach

\[ G(\theta) = \frac{\mu mg}{\cos \theta + \mu \sin \theta} - F \]

def gfn(angle, mu = 0.75, W = 25, F = 17.5):
  theta = math.radians(angle)
  return (mu * W / (math.cos(theta) + mu * math.sin(theta))) - F

gfn(angle = 80)

20.553486370758943

import numpy as np
def bisection(fn, x0, x1, tol=1e-5):
  for i in np.arange(100):
    y0 = fn(x0)
    y1 = fn(x1)
    xm = (x0 + x1)/2
    ym = fn(xm)

    if y0 * ym < 0:
      x1 = xm
    else:
      x0 = xm

    if abs(ym) < tol:
      return xm, i + 1

theta, iter = bisection(gfn, 45, 80)
print("After {} iterations, the angle is {} ".format(iter, theta))

After 14 iterations, the angle is 67.87261962890625 

Newton Raphson Method

The general form of Taylor series is given by the following equation.

\[ P(x) = f(a) + \frac{df(a)}{dx}\frac{(x-a)^1}{1!} + \frac{d^2f(a)}{dx^2}\frac{(x-a)^2}{2!} + \cdots \]

If x = \(\theta_{n+1}\) = \(\theta_n\) + \(\epsilon_n\) and a = \(\theta_n\), then G(\(\theta\))=0 can be approximately as follows.

\[ G(\theta_{n+1}) = G(\theta_n + \epsilon_n) = 0 = G(\theta_n) + \frac{dG(\theta_n)}{d\theta}\frac{(\epsilon_n)^1}{1!} + \frac{d^2G(\theta_n)}{d\theta^2}\frac{(\epsilon_n)^2}{2!} + \cdots \]

By only using the first derivative term,

\[ G(\theta_n + \epsilon_n) = 0 \approx G(\theta_n)+ \frac{dG(\theta_n)}{d\theta}\epsilon_n \]

\[ \epsilon_n = - \frac{G(\theta_n)}{dG(\theta_n)/d\theta} \]

Hence

\[ \theta_{n+1} = \theta_n + \epsilon_n = \theta_n - \frac{G(\theta_n)}{dG(\theta_n)/d\theta} \]

If the gradient dG(\(\theta\))/dx is known, then the above equation can be used iteratively from an initial guess \(\theta_0\) to find \(\theta\) that satisfies G(\(\theta\))=0. The iteration can stop when \(|\epsilon_n|\) becomes smaller than the predefined tolarance.

The first derivate of G(\(\theta\)) is given as follpws.

\[ dG(\theta)/d(\theta) = \frac{\mu mg (\sin \theta - \mu \cos \theta)}{(\cos \theta + \mu \sin \theta)^2} \]

Taylor’s series is used for the cosin and sin functions.

\[ \cos(\theta) \approx cos(0) - cos(0)\frac{\theta^2}{2!} + cos(0)\frac{\theta^4}{4!} + \cdots \]

\[ \sin(\theta) \approx cos(0)\frac{\theta}{1!} - cos(0)\frac{\theta^3}{3!} + \cdots \]

Differentiation

\[ G(\theta) = \frac{\mu W}{\cos \theta + \mu \sin \theta} - F \]

\[G'(\theta) = \frac{\mu W (\sin \theta - \mu \cos \theta)}{(\cos \theta + \mu \sin \theta)^2}\]

import sympy as sym

mu = sym.Symbol('mu')
W = sym.Symbol('W')
theta = sym.Symbol('theta')

g = mu * W / (sym.cos(theta) + mu * sym.sin(theta))
dg = sym.diff(g, theta)
dg

\[\displaystyle \frac{W \mu \left(- \mu \cos{\left(\theta \right)} + \sin{\left(\theta \right)}\right)}{\left(\mu \sin{\left(\theta \right)} + \cos{\left(\theta \right)}\right)^{2}}\]

def dgn(angle, W = 25, mu = 0.75):
  theta = math.radians(angle)
  return (W * mu * (-mu * math.cos(theta) + math.sin(theta))/(mu * math.sin(theta) + math.cos(theta))**2)

dgn(45)

2.164612595469021

def gfn(theta, mu = 0.75, W = 25, F = 17.5):
  return (mu * W / (math.cos(theta) + mu * math.sin(theta))) - F

from scipy.misc import derivative

derivative(gfn, math.radians(45), dx=1e-6, n=1)

2.1646125958341145

def newton(fn, x, tol=1e-5):
  for i in np.arange(100):
    fx = fn(x)
    dfx = derivative(fn, x, dx=1e-6, n=1)
    h = fx / dfx
    x = x - h
    if abs(h) < tol:
      break
  return x, i

angle, iter = newton(gfn, math.radians(60))
print("After {} iterations the solution is {}".format(iter, math.degrees(angle)))

After 3 iterations the solution is 67.87261678062136